Research on the Effectiveness of Different Outlier Detection Methods in Common Data Distribution Types

Qingqing Song; Shaoliang Xia

doi:10.5281/zenodo.10888672

Authors

Qingqing Song Belarusian State University
Shaoliang Xia Belarusian State University

DOI:

https://doi.org/10.5281/zenodo.10888672

References:

25

Keywords:

Outlier Detection, Outlier Analysis, Machine Learning, Data Distribution, Performance Evaluation, Data Preprocessing

Abstract

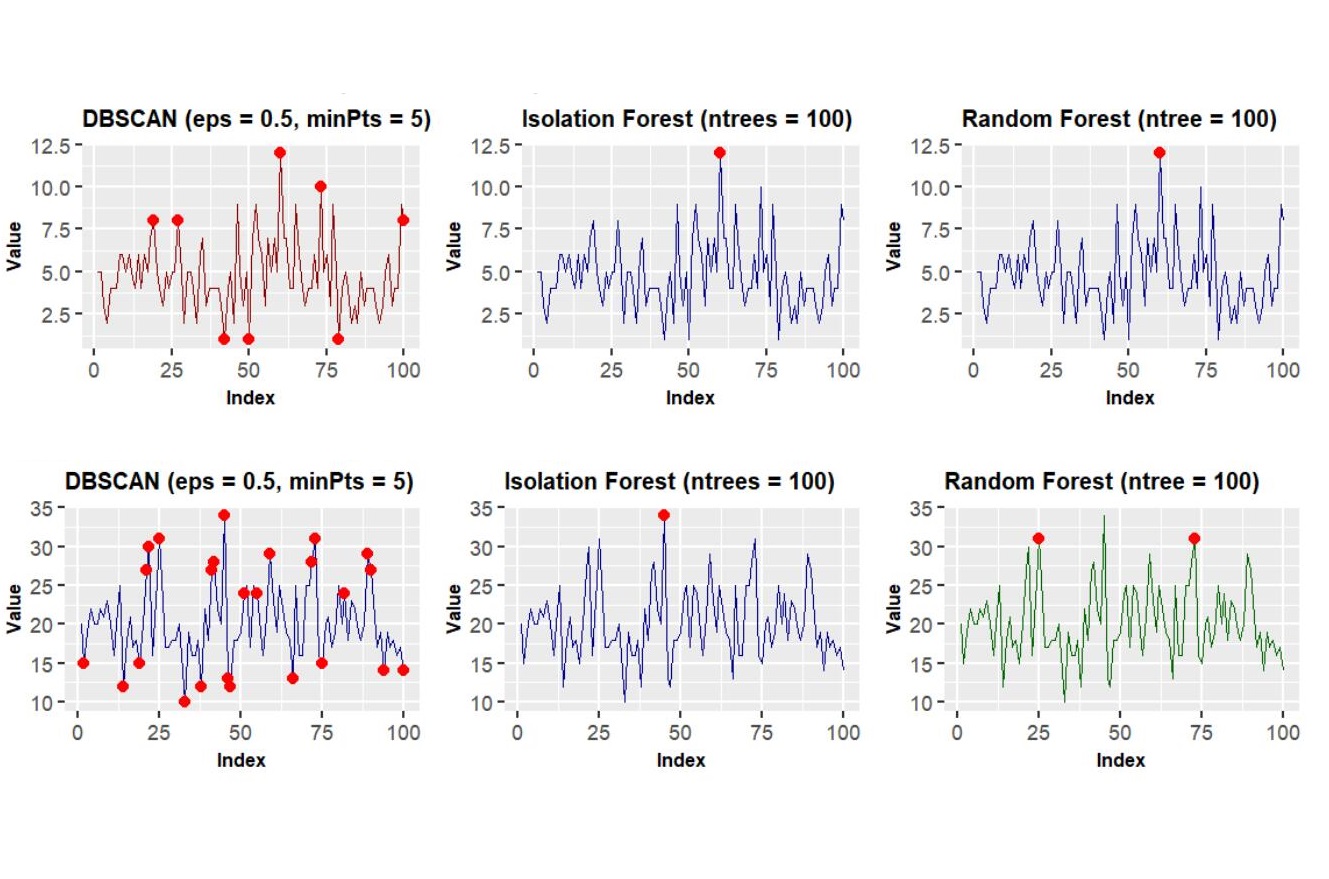
Outlier detection are widely applied in areas such as network performance optimization and pre-processing of machine learning data. In the field of machine learning, the objective is to enhance data quality, thereby improving the performance of subsequent statistical analyses or machine learning models. Currently, there are numerous effective and reliable outlier analysis methods, and their effectiveness varies significantly when dealing with different types of data distributions. Therefore, it is essential to select an appropriate outlier analysis method. In this study, we conducted outlier detection on sample data from five continuous probability distributions (including Normal, Chi-square, Exponential, Gamma, and T distributions) and four discrete probability distributions (including Binomial, Poisson, Geometric, and Hypergeometric distributions). This paper employs five outlier detection methods, namely Z-Score, IQR, DBScan, Isolation Forest, and Random Forest, and evaluates the detection effectiveness of these methods. Through comparison and analysis, this paper summarizes the characteristics of various outlier detection methods when dealing with sample data from different types of distributions. These findings will assist us in making more rational method selections when facing different outlier detection scenarios.

Author Biographies

Qingqing Song, Belarusian State University

Faculty of Applied Mathematics and Computer Science; Belarusian State University; 4 Nezavisimosti Avenue, Minsk 220030, Belarus; e-mails: fpm.sunC@bsu.by

Shaoliang Xia, Belarusian State University

Faculty of Applied Mathematics and Computer Science; Belarusian State University; 4 Nezavisimosti Avenue, Minsk 220030, Belarus; e-mails: fpm.sya@bsu.by

References

Boukerche, A., Zheng, L., & Alfandi, O. (2020). Outlier detection: Methods, models, and classification. ACM Computing Surveys (CSUR), 53(3), 1-37.

Shiffler, R. E. (1988). Maximum Z scores and outliers. The American Statistician, 42(1), 79-80.

Larson, M. G. (2006). Descriptive statistics and graphical displays. Circulation, 114(1), 76-81.

Khan, K., Rehman, S. U., Aziz, K., Fong, S., & Sarasvady, S. (2014, February). DBSCAN: Past, present and future. In The fifth international conference on the applications of digital information and web technologies (ICADIWT 2014) (pp. 232-238). IEEE.

Al Farizi, W. S., Hidayah, I., & Rizal, M. N. (2021, September). Isolation forest based anomaly detection: A systematic literature review. In 2021 8th International Conference on Information Technology, Computer and Electrical Engineering (ICITACEE) (pp. 118-122). IEEE.

Mensi, A., Cicalese, F., & Bicego, M. (2022, May). Using Random Forest Distances for Outlier Detection. In International Conference on Image Analysis and Processing (pp. 75-86). Cham: Springer International Publishing.

Weisstein, E. W. (2002). Normal distribution. https://mathworld. wolfram. com/.

Wilson, E. B., & Hilferty, M. M. (1931). The distribution of chi-square. Proceedings of the National Academy of Sciences, 17(12), 684-688.

Balakrishnan, K. (2019). Exponential distribution: theory, methods and applications. Routledge.

Nadarajah, S. (2011). The exponentiated exponential distribution: a survey. AStA Advances in Statistical Analysis, 95, 219-251.

Thom, H. C. (1958). A note on the gamma distribution. Monthly weather review, 86(4), 117-122.

Lukacs, E. (1955). A characterization of the gamma distribution. The Annals of Mathematical Statistics, 26(2), 319-324.

Ahsanullah, M., Kibria, B. G., & Shakil, M. (2014). Normal and student's t distributions and their applications (Vol. 4). Paris, France:: Atlantis Press.

Weisstein, E. W. (2001). Student's t-Distribution. https://mathworld. wolfram. com/.

Lange, K. L., Little, R. J., & Taylor, J. M. (1989). Robust statistical modeling using the t distribution. Journal of the American Statistical Association, 84(408), 881-896.

Edwards, A. W. F. (1960). The meaning of binomial distribution. Nature, 186(4730), 1074-1074.

Clarke, R. D. (1946). An application of the Poisson distribution. Journal of the Institute of Actuaries, 72(3), 481-481.

Philippou, A. N., Georghiou, C., & Philippou, G. N. (1983). A generalized geometric distribution and some of its properties. Statistics & Probability Letters, 1(4), 171-175.

Skibinsky, M. (1970). A characterization of hypergeometric distributions. Journal of the American Statistical Association, 65(330), 926-929.

Harkness, W. L. (1965). Properties of the extended hypergeometric distribution. The Annals of Mathematical Statistics, 36(3), 938-945.

Kemp, C. D., & Kemp, A. W. (1956). Generalized hypergeometric distributions. Journal of the Royal Statistical Society Series B: Statistical Methodology, 18(2), 202-211.

Goutte, C., & Gaussier, E. (2005, March). A probabilistic interpretation of precision, recall and F-score, with implication for evaluation. In European conference on information retrieval (pp. 345-359). Berlin, Heidelberg: Springer Berlin Heidelberg.

Yacouby, R., & Axman, D. (2020, November). Probabilistic extension of precision, recall, and f1 score for more thorough evaluation of classification models. In Proceedings of the first workshop on evaluation and comparison of NLP systems (pp. 79-91).

Borgonovo, E., & Plischke, E. (2016). Sensitivity analysis: A review of recent advances. European Journal of Operational Research, 248(3), 869-887.

Kleijnen, J. P. (1995). Sensitivity analysis and related analysis: A survey of statistical techniques.